Stephen Scarano

Stephen Scarano

Data Scientist (M.S) with Interests in Artifical Intelligence

Energy Consumption Prediction for Climate Planning

Collaborators: Purva Pruthi, Erin Bartuska, Nelson Evbarunegbe

Working as a Machine Learning Engineer for The University of Massachusetts Center of Data Science (CDS) my team was approached by the Massachusetts Department of Capital Asset Management and Maintenance (DCAMM) to apply data science expertise to their climate initatives. After review, we chose to implement and adapt state-of-the-art time series forecasting to aid long term emission prediction for state-owned buildings. We tried various time-series forecasting approaches (Moving Average, Simple Exponential Smoothing, Holt-Winter’s Exponential Smoothing, Gaussian Process Regression) and provided two methods for 365-day predictions.

  • Holt-Winter’s Exponential Smoothing Holts Winter's plot showing damping and non-damping results for 365-day prediction

Time series data consists of sequences of observations collected over time, composed of trends, seasonality, and irregular fluctuations:

  • Trends: A long-term increase or decrease in the data. This can be seen as a slope (it doesn’t have to be linear) roughly going through the data.
  • Seasonality: A time series is said to be seasonal when it is affected by seasonal factors (hour of day, week, month, year, etc.). Seasonality can be observed with nice cyclical patterns of fixed frequency.
  • Cyclicity: A cycle occurs when the data exhibits rises and falls that are not of a fixed frequency.
  • Residuals: The difference between an observation and its predicted value at each time step.

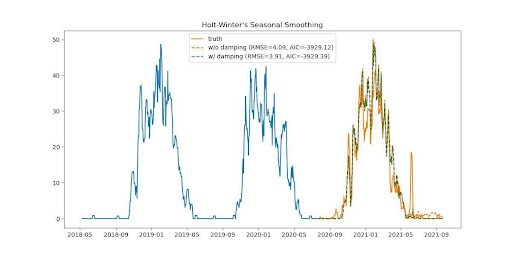
Holt-Winter’s includes a seasonality component along with level and trend components, working best when data has clear linear trend and seasonality. The figure above shows results for a candidate meter with and without damping, i.e decaying the linear trend over time.

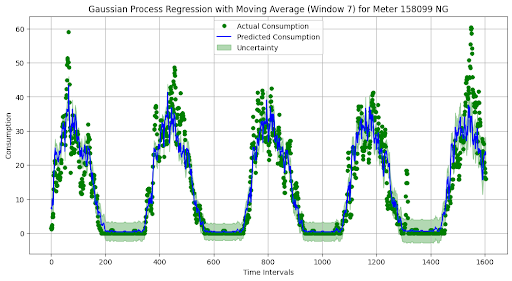
  • Gaussian Process Regression Gaussian Regression plot showing damping and non-damping results for 365-day prediction

Gaussian processes are a non-parametric supervised learning method often applied to regression problems. Our choice to apply GP to meter data was motivated by (1) the ability to perform under uncertainty while modeling and (2) the capacity to determine the uncertainty of a prediction.

As a result, our GP model serves the additional use of outlier detection, i.e the identification of unusual or unexpected data trends which may contribute to unnecessary energy expenditure.